1.3.4: Missing Data and Sampling Weights (brief intro)

(In Person)

Session Objectives (updated)

  1. Identify, summarize and visualize missing data.
  2. Missing Data Mechanisms (bias mechanisms or models)
  3. Missing Data Handling and Imputation Methods (brief intro)
  4. Impact of Sampling Weights for Survey Data (brief intro)

0. Prework - Before You Begin

A. Install packages

If you do not have them already, install the following packages from CRAN (using the RStudio Menu “Tools/Install” Packages interface):

B. Review these online Book Chapters:

C. Open/create an RStudio project for this lesson

Let’s start with the myfirstRproject RStudio project you created in Module 1.3.2 - part 1. If you have not yet created this myfirstRproject RStudio project, go ahead and create a new RStudio Project for this lesson. Feel free to name your project whatever you want, it does not need to be named myfirstRproject.

1. Identify, summarize and visualize missing data

Find Missing Data in Your Dataset.

One simple way to find missing data is to open it in the Data Viewer window and sort the data.

For example, load the VIM package and take a look at the sleep dataset provided within this package.

library(VIM)
data("sleep")

Click on the sleep dataset to open it in the data viewer:

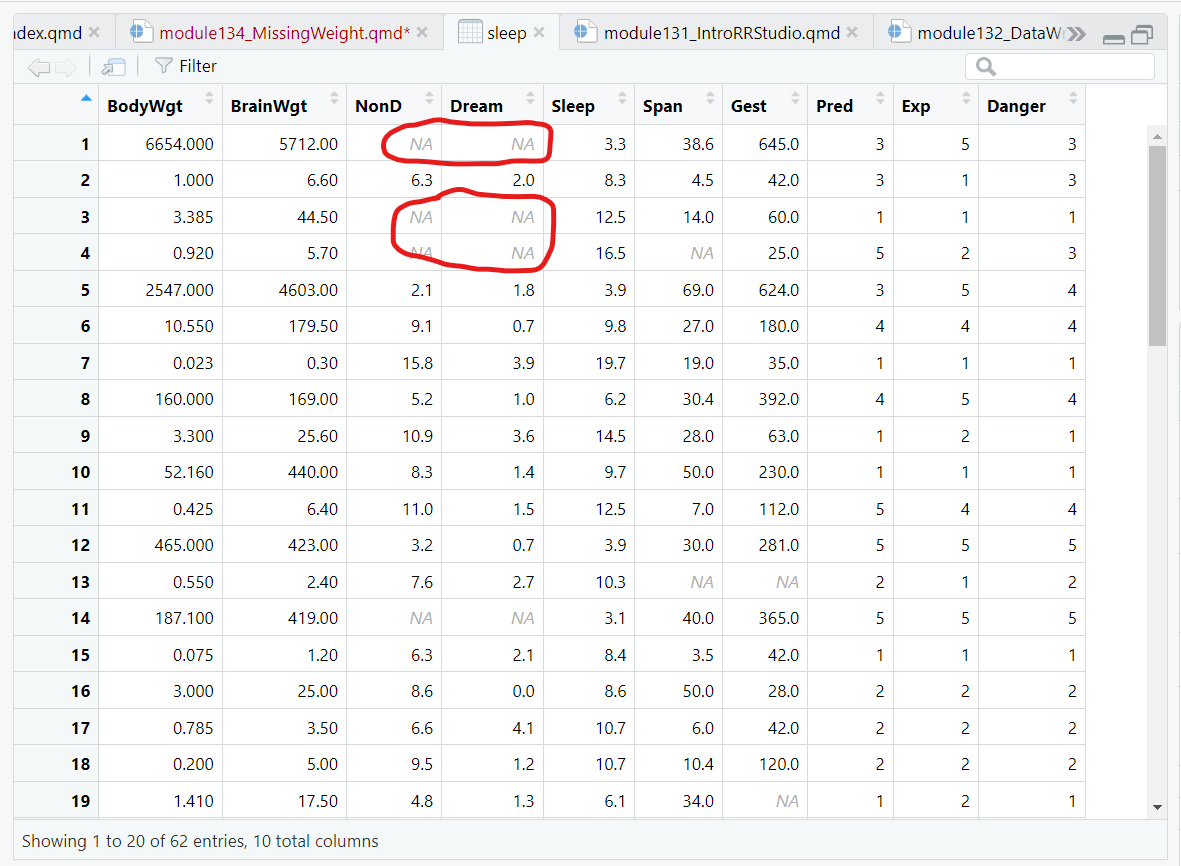
Notice the light grey NAs shown for the missing data spots in this dataset.

If we click on the column for the Dream variable and sort these values, notice that the NAs all now show up at the bottom of the viewer window. It does not matter if you sort ascending or descending, the NAs are always at the bottom of the viewer.

This method is ok for a small dataset with not too many variables or rows of data. But let’s look at other ways to summarize the amounts of missing data in your dataset.

Describe Missing Data.

Built-in summary() function

As we saw back in Module 1.3.2, Section 5, we can use the summary() function to get some basic statistics for each variable in the dataset, including the number of NAs.

summary(sleep)
    BodyWgt            BrainWgt            NonD            Dream      
 Min.   :   0.005   Min.   :   0.14   Min.   : 2.100   Min.   :0.000  
 1st Qu.:   0.600   1st Qu.:   4.25   1st Qu.: 6.250   1st Qu.:0.900  
 Median :   3.342   Median :  17.25   Median : 8.350   Median :1.800  
 Mean   : 198.790   Mean   : 283.13   Mean   : 8.673   Mean   :1.972  
 3rd Qu.:  48.203   3rd Qu.: 166.00   3rd Qu.:11.000   3rd Qu.:2.550  
 Max.   :6654.000   Max.   :5712.00   Max.   :17.900   Max.   :6.600  
                                      NA's   :14       NA's   :12     
     Sleep            Span              Gest             Pred      
 Min.   : 2.60   Min.   :  2.000   Min.   : 12.00   Min.   :1.000  
 1st Qu.: 8.05   1st Qu.:  6.625   1st Qu.: 35.75   1st Qu.:2.000  
 Median :10.45   Median : 15.100   Median : 79.00   Median :3.000  
 Mean   :10.53   Mean   : 19.878   Mean   :142.35   Mean   :2.871  
 3rd Qu.:13.20   3rd Qu.: 27.750   3rd Qu.:207.50   3rd Qu.:4.000  
 Max.   :19.90   Max.   :100.000   Max.   :645.00   Max.   :5.000  
 NA's   :4       NA's   :4         NA's   :4                       
      Exp            Danger     
 Min.   :1.000   Min.   :1.000  
 1st Qu.:1.000   1st Qu.:1.000  
 Median :2.000   Median :2.000  
 Mean   :2.419   Mean   :2.613  
 3rd Qu.:4.000   3rd Qu.:4.000  
 Max.   :5.000   Max.   :5.000

skimr package

Another helpful package is the skimr package which has the skim() function which provides a count of the amount of missing data and the proportion of complete data for that variable.

Rmarkdown for skimr package

When “knitting” to HTML the code below creates the summary table with the miniture histograms. However, when “knitting” to PDF (using the default portrait layout) the histograms get cutoff on the page. Additional LaTex customization is needed to change the layout to landscape to be able to see the histograms.

Data summary
Name sleep
Number of rows 62
Number of columns 10
_______________________
Column type frequency:
numeric 10
________________________
Group variables None

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
BodyWgt 0 1.00 198.79 899.16 0.00 0.60 3.34 48.20 6654.0 ▇▁▁▁▁
BrainWgt 0 1.00 283.13 930.28 0.14 4.25 17.25 166.00 5712.0 ▇▁▁▁▁
NonD 14 0.77 8.67 3.67 2.10 6.25 8.35 11.00 17.9 ▅▇▆▃▂
Dream 12 0.81 1.97 1.44 0.00 0.90 1.80 2.55 6.6 ▇▇▃▁▁
Sleep 4 0.94 10.53 4.61 2.60 8.05 10.45 13.20 19.9 ▅▅▇▃▃
Span 4 0.94 19.88 18.21 2.00 6.62 15.10 27.75 100.0 ▇▃▁▁▁
Gest 4 0.94 142.35 146.81 12.00 35.75 79.00 207.50 645.0 ▇▃▁▁▁
Pred 0 1.00 2.87 1.48 1.00 2.00 3.00 4.00 5.0 ▇▇▆▃▇
Exp 0 1.00 2.42 1.60 1.00 1.00 2.00 4.00 5.0 ▇▃▁▂▃
Danger 0 1.00 2.61 1.44 1.00 1.00 2.00 4.00 5.0 ▇▆▅▅▃

modelsummary package

Another helpful package is the modelsummary package which has the datasummary_skim() function which is a slightly better version built off the skimr::skim() package and function.

Unique Missing Pct. Mean SD Min Median Max Histogram
BodyWgt 60 0 198.8 899.2 0.0 3.3 6654.0
BrainWgt 59 0 283.1 930.3 0.1 17.2 5712.0
NonD 40 23 8.7 3.7 2.1 8.4 17.9
Dream 31 19 2.0 1.4 0.0 1.8 6.6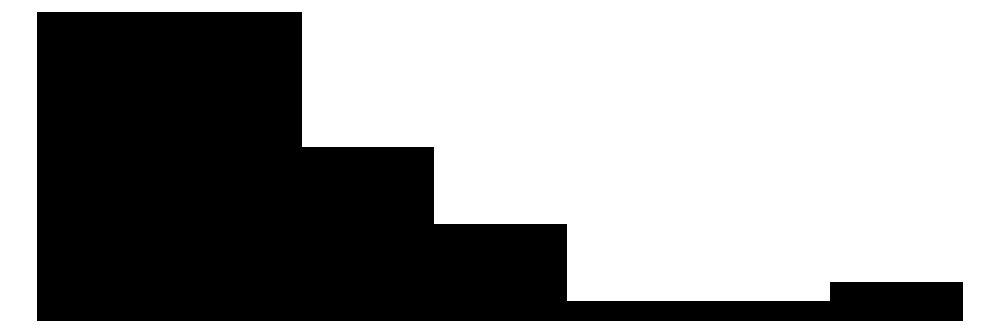
Sleep 45 6 10.5 4.6 2.6 10.4 19.9
Span 48 6 19.9 18.2 2.0 15.1 100.0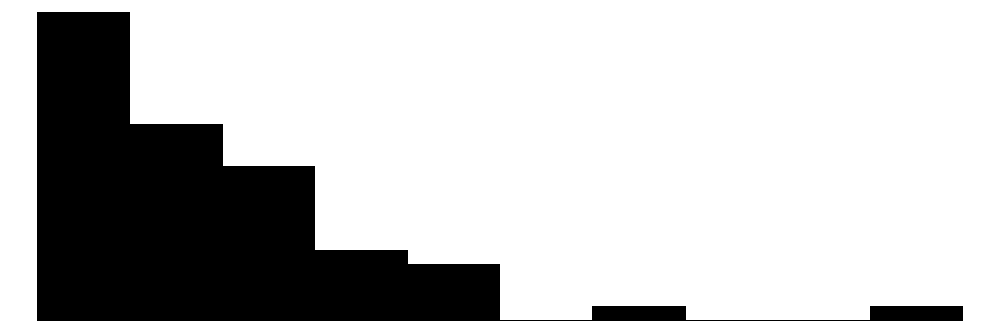
Gest 50 6 142.4 146.8 12.0 79.0 645.0
Pred 5 0 2.9 1.5 1.0 3.0 5.0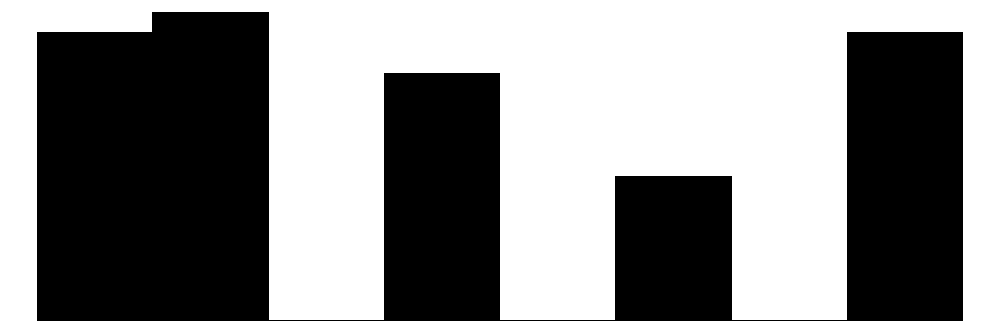
Exp 5 0 2.4 1.6 1.0 2.0 5.0
Danger 5 0 2.6 1.4 1.0 2.0 5.0

summarytools package

Another package that also provides a nice summary of the variables in the dataset, is the dfSummary() from the summarytools dataset.

NOTE: Learn more about how to use summarytools::dfSummary() in an Rmarkdown document at https://cran.r-project.org/web/packages/summarytools/vignettes/rmarkdown.html.

Try It On Your Own

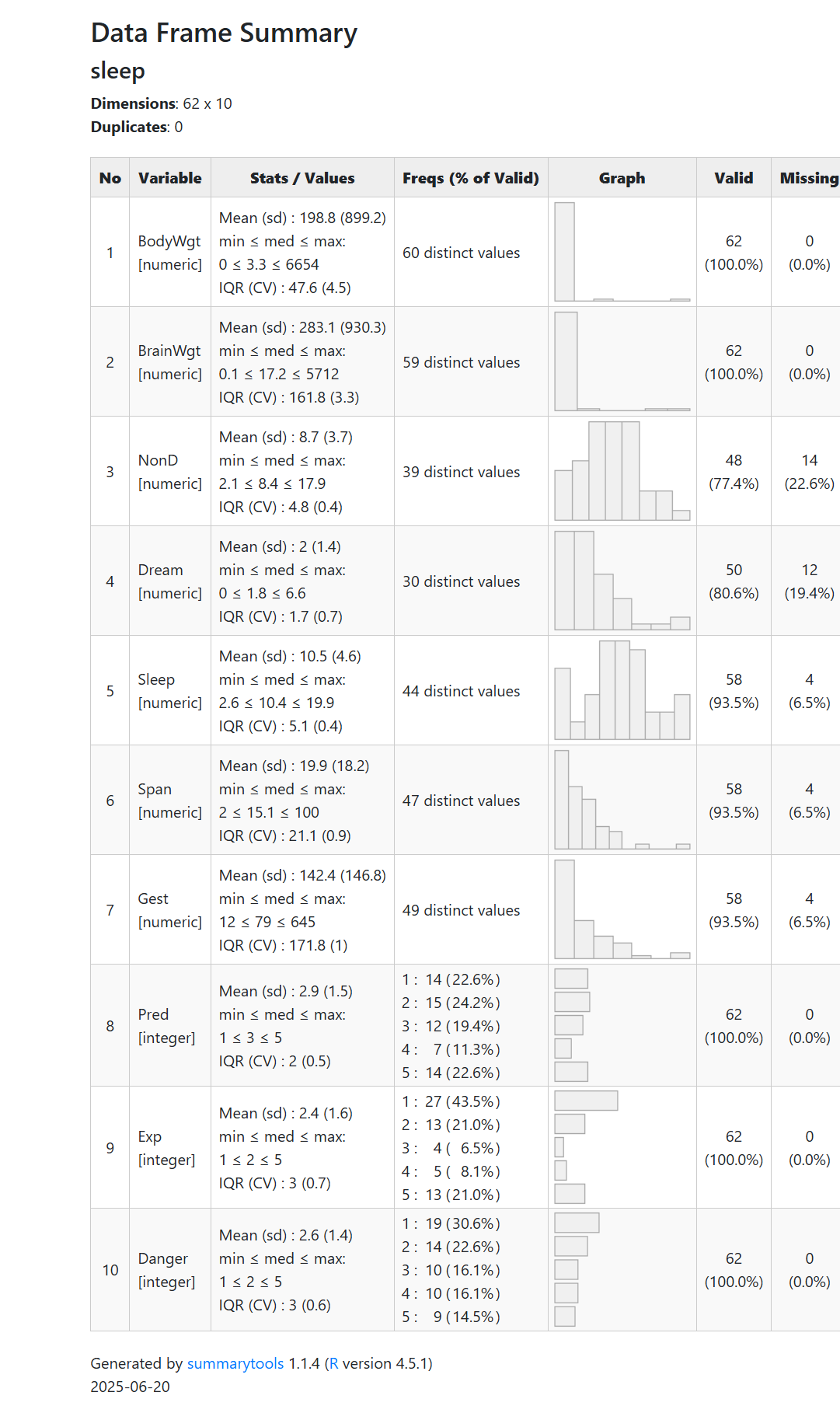
Try running summary() or skim() on the penguins dataset from the palmerpenguins package. Notice the summaries for the numeric and the factor type variables.

      species          island    bill_length_mm  bill_depth_mm  
 Adelie   :152   Biscoe   :168   Min.   :32.10   Min.   :13.10  
 Chinstrap: 68   Dream    :124   1st Qu.:39.23   1st Qu.:15.60  
 Gentoo   :124   Torgersen: 52   Median :44.45   Median :17.30  
                                 Mean   :43.92   Mean   :17.15  
                                 3rd Qu.:48.50   3rd Qu.:18.70  
                                 Max.   :59.60   Max.   :21.50  
                                 NA's   :2       NA's   :2      
 flipper_length_mm  body_mass_g       sex           year     
 Min.   :172.0     Min.   :2700   female:165   Min.   :2007  
 1st Qu.:190.0     1st Qu.:3550   male  :168   1st Qu.:2007  
 Median :197.0     Median :4050   NA's  : 11   Median :2008  
 Mean   :200.9     Mean   :4202                Mean   :2008  
 3rd Qu.:213.0     3rd Qu.:4750                3rd Qu.:2009  
 Max.   :231.0     Max.   :6300                Max.   :2009  
 NA's   :2         NA's   :2                                 
skim(penguins)
Data summary
Name penguins
Number of rows 344
Number of columns 8
_______________________
Column type frequency:
factor 3
numeric 5
________________________
Group variables None

Variable type: factor

skim_variable n_missing complete_rate ordered n_unique top_counts
species 0 1.00 FALSE 3 Ade: 152, Gen: 124, Chi: 68
island 0 1.00 FALSE 3 Bis: 168, Dre: 124, Tor: 52
sex 11 0.97 FALSE 2 mal: 168, fem: 165

Variable type: numeric

skim_variable n_missing complete_rate mean sd p0 p25 p50 p75 p100 hist
bill_length_mm 2 0.99 43.92 5.46 32.1 39.23 44.45 48.5 59.6 ▃▇▇▆▁
bill_depth_mm 2 0.99 17.15 1.97 13.1 15.60 17.30 18.7 21.5 ▅▅▇▇▂
flipper_length_mm 2 0.99 200.92 14.06 172.0 190.00 197.00 213.0 231.0 ▂▇▃▅▂
body_mass_g 2 0.99 4201.75 801.95 2700.0 3550.00 4050.00 4750.0 6300.0 ▃▇▆▃▂
year 0 1.00 2008.03 0.82 2007.0 2007.00 2008.00 2009.0 2009.0 ▇▁▇▁▇

Visualize Missing Data.

Making plots with VIM package

The VIM package has an “aggregate” function aggr() which counts up the amounts of missing data for each variable and combinations of variables. The sleep dataset only has 10 variables.

WARNING - Beware of Using Too Many Variables at Once

Before using the aggr() function, limit the number of variables. FIRST create a dataset with only the variables you are interested in BEFORE running the function - otherwise you may lock up your computer if you feed it too many variables at once.

# get the amount of missing data in the sleep dataset
a <- aggr(sleep, plot = FALSE)
a

 Missings in variables:
 Variable Count
     NonD    14
    Dream    12
    Sleep     4
     Span     4
     Gest     4

The default output from above only lists the variables that have one or more rows with missing data. However, you can get a list of all of the variables with this code:

a$missings
         Variable Count
BodyWgt   BodyWgt     0
BrainWgt BrainWgt     0
NonD         NonD    14
Dream       Dream    12
Sleep       Sleep     4
Span         Span     4
Gest         Gest     4
Pred         Pred     0
Exp           Exp     0
Danger     Danger     0

Next, let’s get some plots of the missing data in the sleep dataset.

The plot on the LEFT below is a simple bar plot showing the missing counts for each variable in the dataset. Notice that there are only 5 variables with one or more missing values:

  • NonD
  • Dream
  • Sleep
  • Span
  • Gest

The plot on the RIGHT however, shows the amounts of missing data for the various patterns of missing data for the 10 variables in the sleep dataset. For example, notice that of the 62 rows of data in the sleep dataset:

  • there are only 42 rows with complete data with no missing data on all 10 variables (i.e., 42/62 = 67.7% of the data is complete for all 10 variables);
  • the next largest “pattern” of missing data is 9 rows that have both NonD and Dream variables with missing values; and
  • there are 3 rows of data with the gest variable having missing data.
# make plots of the amounts and patterns of missing data
plot(a, numbers = TRUE, prop = FALSE)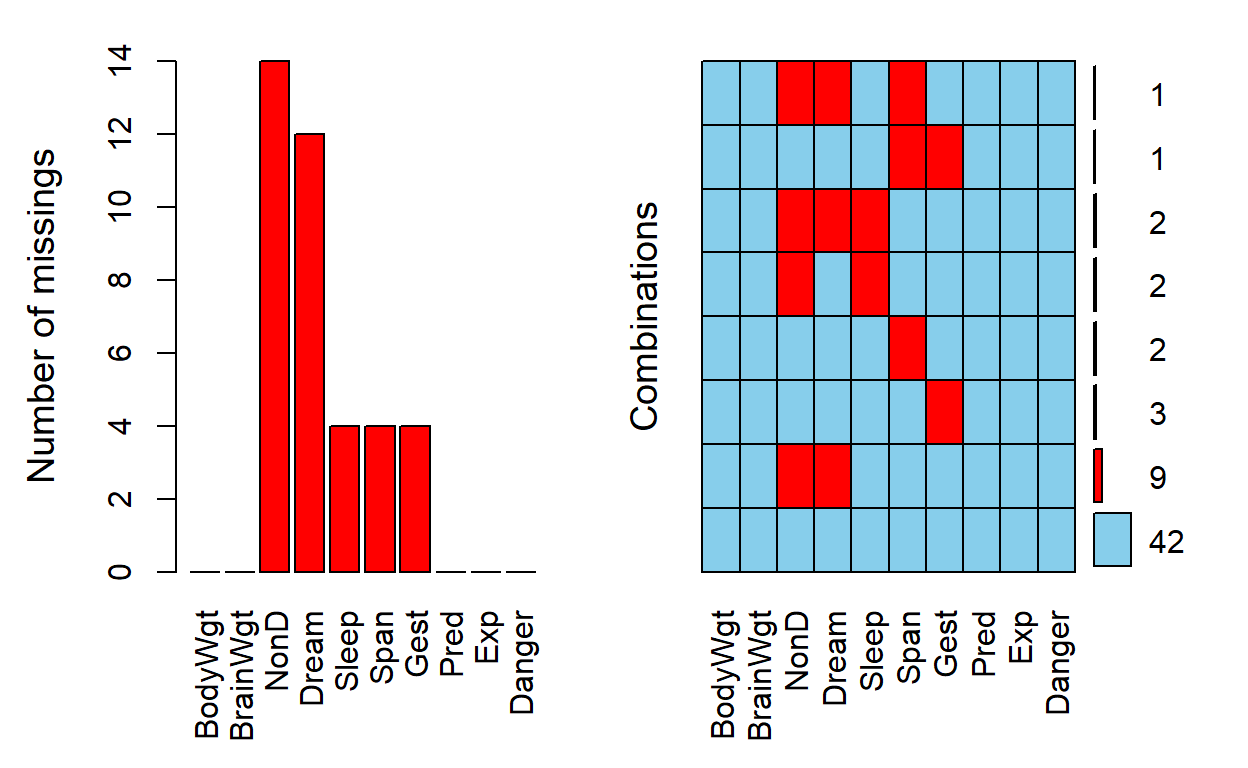

Exploring patterns of missingness can be informative to better understand why the data might be missing and possibly provide insights into the underlying mechanisms causing or leading to the missing data.

Marginplots - see how missingness varies with other measures

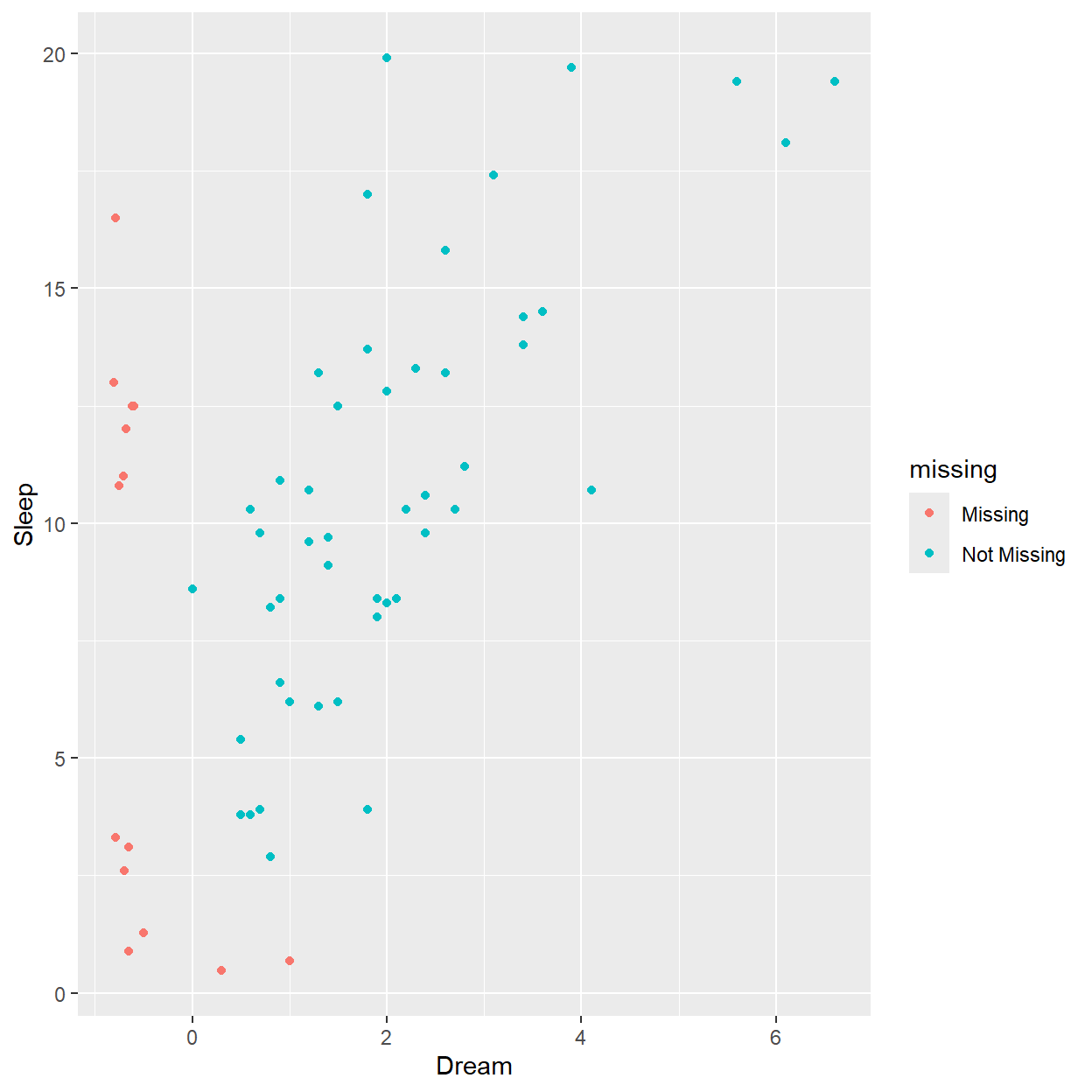
In addition to a usual scatterplot, the marginplot() function in the VIM package, also shows information about missing values in the plot margins.

The red boxplot on the left shows the distrubution of all values of Sleep where Dream contains a missing value. The blue boxplot on the left shows the distribution of the values of Sleep where Dream is observed.

x <- sleep[, c("Dream", "Sleep")]
marginplot(x)

Visualize Missing Data with the naniar package

The naniar package “provides principled, tidy ways to summarise, visualise, and manipulate missing data with minimal deviations from the workflows in ggplot2 and tidy data.” See naniar website.

For example, let’s make a similar to plot to what we did above to visualize the scatterplot between Dream and Sleep but also consider the amounts of missing data of one variable relative to the other variable in the plot. We can do this using the geom_miss_point() function provided in the naniar package which works with ggplot2.

library(naniar)
library(ggplot2)

ggplot(sleep, 
       aes(x = Dream, 
           y = Sleep)) + 
  geom_miss_point()

We can also create an UpSet plot which is useful for visualizing intersections between sets. In the case of missing data, we are interested in visualizing how the missing data for each variable overlaps with each other (i.e., the missing data patterns).

To create an UpSet plot for the missing data patterns for the 10 variables in the sleep dataset, we can use the gg_miss_upset() function. The plot produced is similar to the plot above from the VIM package.

Notice that the plot ONLY shows patterns for the 20 of 62 rows and for the 5 of 10 variables with any missing data. The plot shows that:

  • 9 rows have missing data for both the Dream and NonD variables
  • 3 rows have missing data for the Gest variable
  • 2 rows have missing data for the Span variable
  • 2 rows have missing data for both Sleep and NonD
  • 2 rows have missing data for Sleep, Dream and NonD variables
  • 1 row has missing data for both Span and Gest
  • 1 row has missing data for Span, Dream and NonD variables

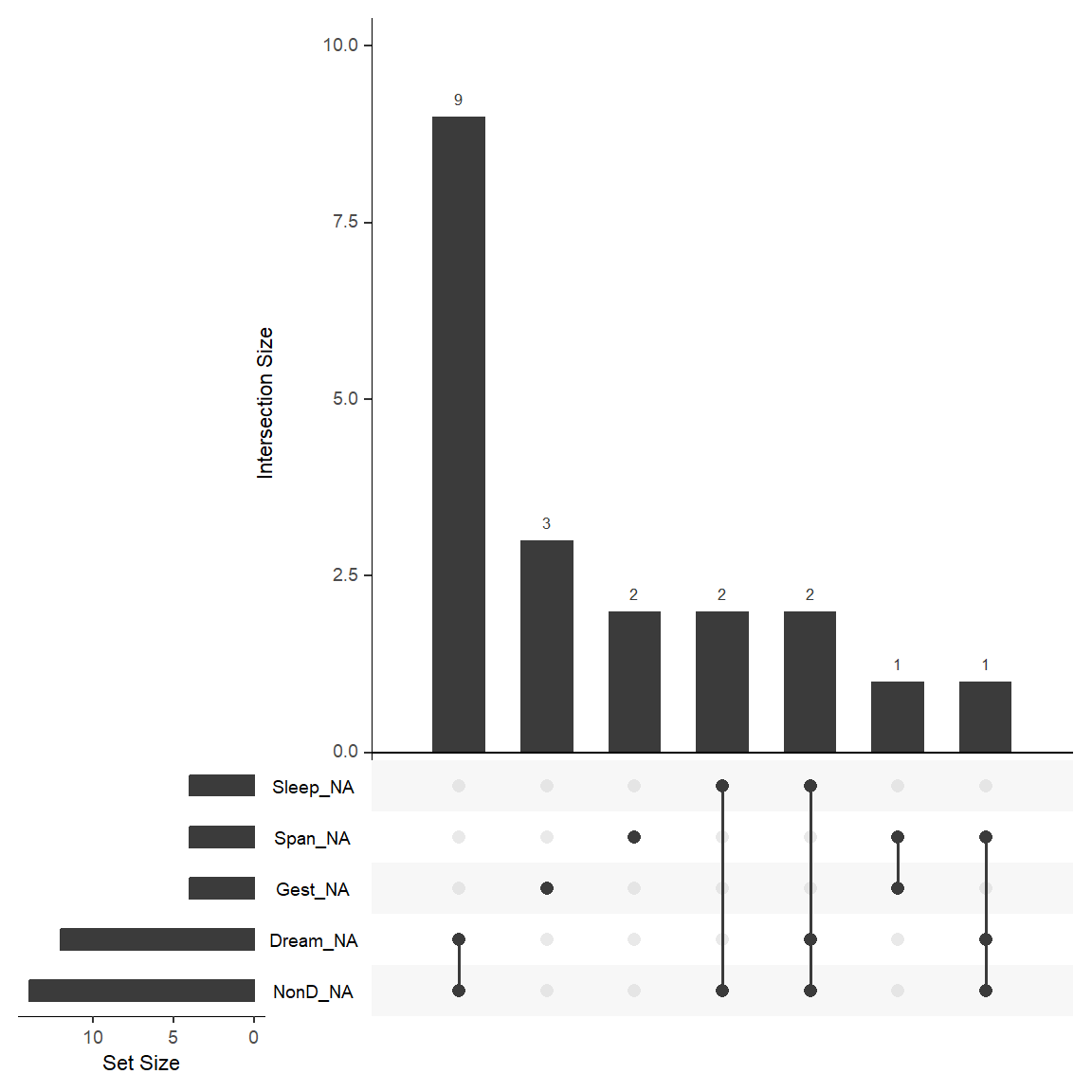
2. Missing Data Mechanisms (bias mechanisms or models)

Why should we worry about missing data?

Setting aside bias concerns for the moment, missing data logistically causes issues with code - especially in R. At first glance this seems to be a huge pain since we get errors or nonsensical output. But these issues force us to deal with the missing data and provide explicit instructions to the computer code on how we want to address the missing data. Learn more in the Flexible Imputation of Missing Data BOOK.

Impact of missing data for descriptive stats like the mean

For example, let’s find the mean of the Dream variable in the sleep dataset.

mean(sleep$Dream)
[1] NA

We get NA since there is missing data for the Dream variable, thus the mean of all rows is “not available”. So, we need to tell R to first remove the missing values (the NAs) prior to computing the mean.

mean(sleep$Dream, na.rm = TRUE)
[1] 1.972

Impact of missing data for summary statistics

We did do a deep dive above and we know that there are 12 rows with missing values for the Dream variable. But if we had run the mean() function with na.rm = TRUE, we might not have know just how much data was missing. So, it is always a good idea to make sure to check for missing data and assess how much you have PRIOR to conducting any analyses.

As we saw in Module 1.3.2, section 5 we can use the gtsummary package with the tbl_summary() function to get better summary statistics including a list of the amount of unknown (missing) rows. Let’s get the means (and standard deviations) for 3 of the variables in the sleep dataset. Notice that there are no “unknowns” for BrainWgt since it has no missing values.

Customizing gtsummary::tbl_summary()

Learn more at Multiline Summaries Using tbl_summary() on how I customized this table to include the count (N) of non-missing rows, mean and standard deviation along with the counts for the unknowns.

library(dplyr)
library(gtsummary)

sleep %>%
  select(Dream, Gest, BrainWgt) %>%
  tbl_summary(
    type = all_continuous() ~ "continuous2",
    statistic = all_continuous() ~ c(
      "{N_nonmiss}",
      "{mean} ({sd})"
    )
  )
Characteristic N = 62
Dream
    N Non-missing 50
    Mean (SD) 1.97 (1.44)
    Unknown 12
Gest
    N Non-missing 58
    Mean (SD) 142 (147)
    Unknown 4
BrainWgt
    N Non-missing 62
    Mean (SD) 283 (930)

Impact of missing data for regression models

When running a model, like a regression model between Dream and Sleep, let’s look at the summary output from fitting a linear model using the built-in lm() function:

summary(lm(Sleep ~ Dream, data = sleep))

Call:
lm(formula = Sleep ~ Dream, data = sleep)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2765 -2.0384 -0.1096  2.1599  9.2624 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.0273     0.7960   7.572 1.27e-09 ***
Dream         2.3051     0.3209   7.183 4.85e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.178 on 46 degrees of freedom
  (14 observations deleted due to missingness)
Multiple R-squared:  0.5287,    Adjusted R-squared:  0.5184 
F-statistic: 51.59 on 1 and 46 DF,  p-value: 4.849e-09

Notice the output tells us that (14 observations deleted due to missingness). So this model was fit with only 62-14 = 48 rows (77.4%) of the original 62 rows of data. The model was fit using only the complete dataset based on the 2 variables in the model: Dream and Sleep, where

  • there are 10 rows missing data for only the Dream variable,
  • 2 rows missing data for both Dream and Sleep variables,
  • and 2 rows missing data for only the Sleep variable.

Keep in mind, when you are fitting any model (linear or logistic regression, analysis of variance, etc), the default is (almost) always to use a LISTWISE deletion, which removes ALL rows with any missing data on any of the variables considered in the model - including predictors, covariates, and outcome(s).

Impact of missing data for correlation matrix - cor() function

Let’s also look at a small correlation matrix considering PAIRWISE versus LISTWISE deletion of missing data for 3 variables from the sleep dataset. Notice that the correlation between BrainWgt and Dream and Sleep are slightly different between LISTWISE and PAIRWISE approaches. These are all pearson correlations by default.

LISTWISE deletion

# LISTWISE deletion, use = "complete.obs"
sleep %>%
  select(BrainWgt, Dream, Sleep) %>%
  cor(use = "complete.obs")
            BrainWgt       Dream      Sleep
BrainWgt  1.00000000 -0.08437367 -0.3221748
Dream    -0.08437367  1.00000000  0.7270870
Sleep    -0.32217479  0.72708696  1.0000000

PAIRWISE deletion

# PAIRWISE deletion, use = "pairwise.complete.obs"
sleep %>%
  select(BrainWgt, Dream, Sleep) %>%
  cor(use = "pairwise.complete.obs")
           BrainWgt      Dream     Sleep
BrainWgt  1.0000000 -0.1051388 -0.358102
Dream    -0.1051388  1.0000000  0.727087
Sleep    -0.3581020  0.7270870  1.000000

Impact of missing data for correlation matrix - Hmisc package

There is also a helpful correlation function rcorr() in the Hmisc package. From this function we can save the output and get the n’s and p-values in addition to the (Pearson) correlations. These numeric data have to be converted to a numeric matrix prior to inputting them to the rcorr() function, which is why as.matrix() is used in the code chunk below.

NOTE: PAIRWISE deletion is the default setting for Hmisc::rcorr().

library(Hmisc)
c1 <- sleep %>%
  select(BrainWgt, Dream, Sleep) %>%
  as.matrix() %>%
  rcorr()

Show the correlations:

c1$r
           BrainWgt      Dream     Sleep
BrainWgt  1.0000000 -0.1051388 -0.358102
Dream    -0.1051388  1.0000000  0.727087
Sleep    -0.3581020  0.7270870  1.000000

Get the sample sizes for each correlation in the matrix:

c1$n
         BrainWgt Dream Sleep
BrainWgt       62    50    58
Dream          50    50    48
Sleep          58    48    58

Get each individual p-value for each correlation:

c1$P
            BrainWgt        Dream        Sleep
BrainWgt          NA 4.674359e-01 5.779531e-03
Dream    0.467435869           NA 4.849120e-09
Sleep    0.005779531 4.849120e-09           NA
Getting complete data

Note: The rcorr() function uses a PAIRWISE missing values deletion approach. If we want the LISTWISE correlations, we have to get complete data first. Use complete.cases() from the built-in stats package with dplyr::filter() to pull out only the 48 rows in the sleep dataset with complete cases on these 3 variables.

c2 <- sleep %>%
  select(BrainWgt, Dream, Sleep) %>%
  filter(complete.cases(.)) %>% 
  as.matrix() %>%
  rcorr()

Show the correlations:

c2$r
            BrainWgt       Dream      Sleep
BrainWgt  1.00000000 -0.08437367 -0.3221748
Dream    -0.08437367  1.00000000  0.7270870
Sleep    -0.32217479  0.72708696  1.0000000

Get the sample sizes for each correlation in the matrix:

c2$n
         BrainWgt Dream Sleep
BrainWgt       48    48    48
Dream          48    48    48
Sleep          48    48    48

Get each individual p-value for each correlation:

c2$P
           BrainWgt        Dream        Sleep
BrainWgt         NA 5.685642e-01 2.553771e-02
Dream    0.56856416           NA 4.849120e-09
Sleep    0.02553771 4.849120e-09           NA

Missing Data Mechanisms

There are entire books and entire courses dedicated to understanding and dealing with missing data mechanisms, which we will not have time to go into depth in this TIDAL course.

Learn more at:

The 3 missing data mechanisms to know are:

  • MCAR = “missing completely at random”
    • This assumes that the missingness is not related to the data at all.
    • If the probability of being missing is the same for all cases, then the data are said to be missing completely at random (MCAR).
  • MAR = “missing at random”
    • If the probability of being missing is the same only within groups defined by the observed data, then the data are missing at random (MAR).
    • For example, if people with higher levels of depression who were more likely to not answer a question or not complete the study, the the missingness is “dependent” upon depression levels measured in the study.
  • MNAR (or NMAR) = “missing not at random (not missing at random)”
    • MNAR means that the probability of being missing varies for reasons that are unknown to us.
    • An example of MNAR in public opinion research occurs if those with weaker opinions respond less often (e.g., non-response bias).

There is a nice summary of different approaches and assumptions and the effects to the models and statistical estimates, see FIMD Book, Section 1.3.8 Summary. This table illustrates that many “ad hoc” missing imputation approaches can result in standard errors that are too large or too small leading to incorrect calculations for p-values and confidence intervals.

Compare rows with and without missing data

Let’s take a look at the BodyWgt and BrainWgt variables and compare the values for rows with and without missing data for the Dream variable. Here are the steps involved:

  1. Create an indicator variable where 0=not missing and 1=missing for the Dream variable.
  2. Run comparisons for the rows (subjects) with and without missing Dream data.
  3. Potentially make plots to compare the rows with and without missing values for Dream.

Note: Both BodyWgt and BrainWgt are highly right skewed, so I did a log transform of both. Notice that the p-values for the non-parametric independent group test (Mann Whitney/Wilcoxon Rank Sum test) are the same, since the tests are based on ranks.

# make small dataset
s1 <- sleep %>%
  select(BodyWgt, BrainWgt, Dream)

# add missing indicator
s1$Dream_missing <- as.numeric(is.na(s1$Dream))

# both BodyWgt and BrainWgt are highly right skewed
# do a log transform of both
s1 <- s1 %>%
  mutate(log_BodyWgt = log(BodyWgt),
         log_BrainWgt = log(BrainWgt))

Table comparing BodyWgt and BrainWgt for rows with and without missing Dream data. Both are statistically significant - the animals with missing Dream values are larger (bigger body and brain weights).

s1 %>%
  tbl_summary(
    by = Dream_missing,
    include = c(BodyWgt, log_BodyWgt,
                BrainWgt, log_BrainWgt)
  ) %>%
  add_p()
Characteristic 0
N = 501 		1
N = 121 		p-value2
BodyWgt 2 (0, 28) 25 (4, 144) 0.020
log_BodyWgt 0.61 (-1.27, 3.32) 3.13 (1.31, 4.92) 0.020
BrainWgt 12 (3, 169) 77 (28, 282) 0.041
log_BrainWgt 2.50 (1.10, 5.13) 4.31 (3.25, 5.53) 0.041
1 Median (Q1, Q3)
2 Wilcoxon rank sum test

Side-by-side boxplots for the (log) of BodyWgt for rows with missing Dream data and without.

ggplot(s1, aes(group = Dream_missing,
               y = log_BodyWgt)) +
  geom_boxplot()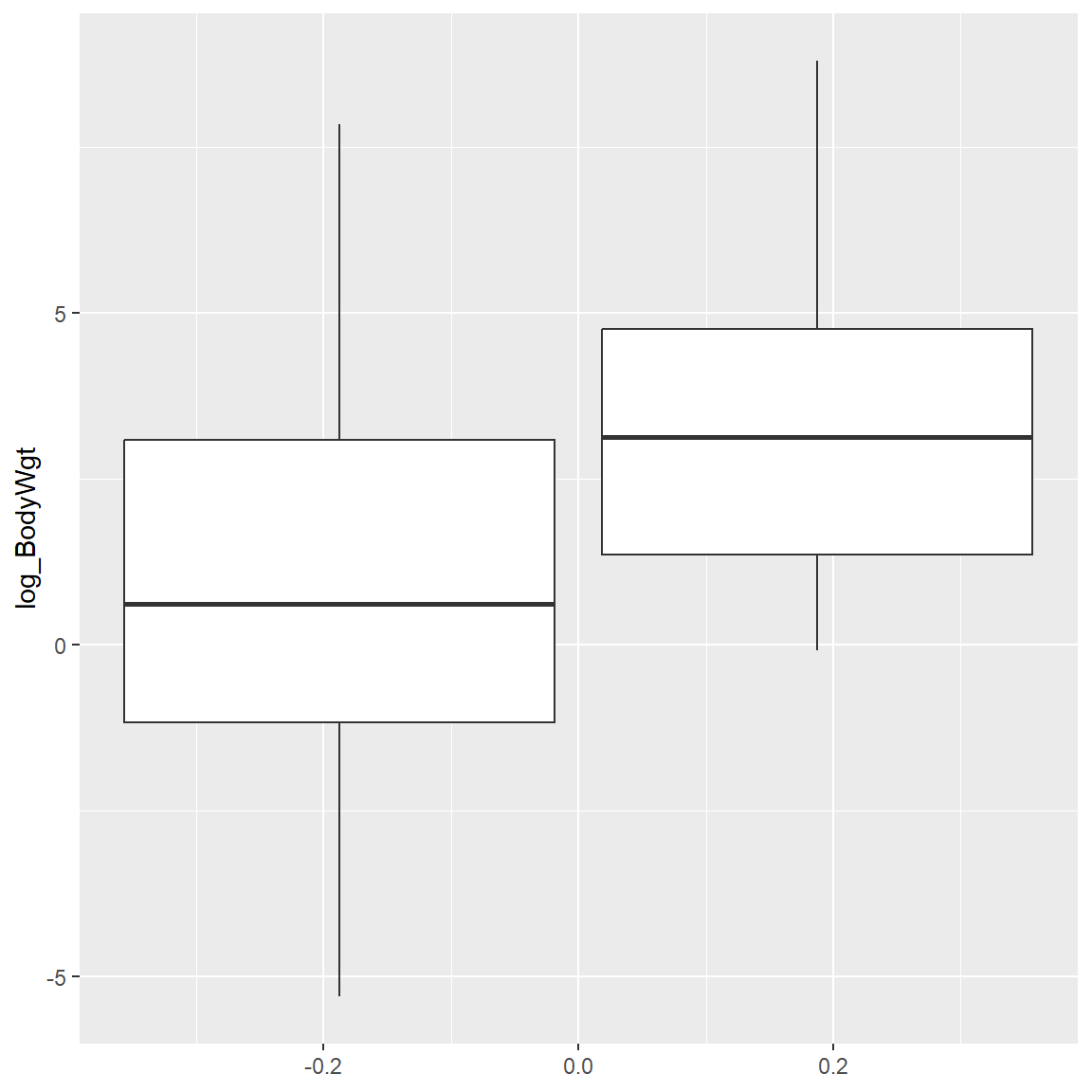

3. Missing Data Handling and Imputation Methods (brief intro)

Imputation - Mean Substitution

There are many ideas and options for creating data to “fill-in” or “impute” the spots for the missing values. Keep in mind that these methods are “making up” new (unobserved) data. Ideally, the missing imputation methods should be as unbiased as possible and should not increase or decrease the variability of the data. As good as some methods may be, always keep in mind that we will never know for sure if these new imputed data are “correct” or if they are the best they can be.

A simple example, suppose we have a variable with 5 numbers. Let’s compute the mean and standard deviation of these numbers.

x <- c(2, 4, 3, 5, 10)
mean(x, na.rm = TRUE)
[1] 4.8
sd(x, na.rm = TRUE)
[1] 3.114482

Now let’s set the 1st value to missing - replace the 2 with NA. Notice that the mean increases and the standard deviation decreased slightly from 3.114 to 3.109.

xna <- c(NA, 4, 3, 5, 10)
mean(xna, na.rm = TRUE)
[1] 5.5
sd(xna, na.rm = TRUE)
[1] 3.109126

Now, let’s take the mean we just computed from the 4 non-missing values which was 5.5 and substitute it in for the missing value and recompute the new mean and standard deviation.

xsub <- c(5.5, 4, 3, 5, 10)
mean(xsub, na.rm = TRUE)
[1] 5.5
sd(xsub, na.rm = TRUE)
[1] 2.692582

IMPORTANT The new mean of xsub is the same = 5.5 as the mean for xna, but the standard deviation for this new list of 5 numbers is much smaller = 2.693 down from 3.109. And this “shrinking” of the standard deviation is even more pronounced from the original 5 numbers which was 3.114 for x. And the mean of the original numbers was 4.8 which is smaller than the mean-subtituted list for xsub.

This is a simple example and illustrates why we don’t want to use mean-substitution for missing data. It also highlights that the goals of missing data imputation ideally shouldn’t cause bias for estimating statistics like the mean and shouldn’t increase or decrease the underlying variance of the original variables. And in theory the new variable with imputed data also shouldn’t change the correlations (relationships) between the variables in the dataset. As you can see this can get complex rapidly and no imputation method is perfect. Often multiple missing inputation methods should be explored and some methods may work better for different models and statistical tests than others.

Commonly accepted use of mean-substitution

The one place where I see mean substitution used often is for survey instruments. For example the CESD (Center for Epidemiological Studies-Depression) which has 20 items with a 4-point Likert-scaled response coded 0, 1, 2, 3.

For this instrument you can compute a valid score from only 16 of the 20 items by taking the mean of these 16 items. This is equivalent to using mean-substitution for the 4 missing responses (e.g. CESD allows up to 20% missing items within a given subject, within a given row of data). But this is ROWWISE mean substitution. The example above is illustrating COLUMNWISE mean substitution.

To avoid mean-substitution bias even for ROWWISE substitution, you ideally want to use this on less than 5%-10% of your sample. If more than 5%-10% of your sample is not completing the survey, there may still be underlying response bias issues that need to be addressed.

Example of k-nearest neighbor (kNN) missing imputation method

Instead of using mean substitution, let’s look at another method - k-nearest neighbor, which is a “donor-based” method. Learn more at:

Let’s take the little dataset x which is a subset of the sleep dataset which has all 62 rows but only the Dream and Sleep variables. For these 2 variables, let’s see what the kNN() (k-nearest neighbor) function in the VIM package does.

x <- sleep[, c("Dream", "Sleep")]
x_imputed <- kNN(x)

Now look at a scatterplot plot for these new Dream and Sleep variables with imputed values from the k-nearest neighbor approach. Notice the coloring of the points - the blue are the original values and the other colors represent the structure of missings.

  • brown points represent values where Dream was missing initially
  • beige points represent values where Sleep was missing initially
  • black points represent values where both Dream and Sleep were missing initially

The kNN() method appears to preserve the correlation between Dream and Sleep.

marginplot(x_imputed, delimiter = "_imp")

kNN imputed values - compare correlations before and after

Let’s compare the results before and after the imputation for correlation and for a simple regression model. This is a “sensitivity” test of sorts. It is always a good idea to compare the results before and after applying any imputation method.

Correlation Original Data:

x %>%
  as.matrix() %>%
  Hmisc::rcorr()
      Dream Sleep
Dream  1.00  0.73
Sleep  0.73  1.00

n
      Dream Sleep
Dream    50    48
Sleep    48    58

P
      Dream Sleep
Dream        0   
Sleep  0

Correlation kNN Imputed Data:

x_imputed %>%
  select(Dream, Sleep) %>%
  as.matrix() %>%
  Hmisc::rcorr()
      Dream Sleep
Dream  1.00  0.74
Sleep  0.74  1.00

n= 62 


P
      Dream Sleep
Dream        0   
Sleep  0

kNN imputed values - compare regression before and after

Simple Linear Regression Original Data:

summary(lm(Sleep ~ Dream, data = x))

Call:
lm(formula = Sleep ~ Dream, data = x)

Residuals:
    Min      1Q  Median      3Q     Max 
-6.2765 -2.0384 -0.1096  2.1599  9.2624 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.0273     0.7960   7.572 1.27e-09 ***
Dream         2.3051     0.3209   7.183 4.85e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.178 on 46 degrees of freedom
  (14 observations deleted due to missingness)
Multiple R-squared:  0.5287,    Adjusted R-squared:  0.5184 
F-statistic: 51.59 on 1 and 46 DF,  p-value: 4.849e-09

Simple Linear Regression kNN Imputed Data:

summary(lm(Sleep ~ Dream, data = x_imputed))

Call:
lm(formula = Sleep ~ Dream, data = x_imputed)

Residuals:
   Min     1Q Median     3Q    Max 
-6.241 -2.283 -0.221  2.157  9.257 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   5.6222     0.6920   8.125 3.00e-11 ***
Dream         2.5106     0.2949   8.512 6.58e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.074 on 60 degrees of freedom
Multiple R-squared:  0.547, Adjusted R-squared:  0.5395 
F-statistic: 72.46 on 1 and 60 DF,  p-value: 6.579e-12

Notice that the correlations were similar. The regression intercepts and slopes were slightly different and the “Std. Error” for the regression coefficients for the imputed model were smaller than for the original data.

Example of multiple missing imputation method (using mice)

Let’s take a look at the mice (Multivariate Imputation by Chained Equations) package. The mice package provides for Multiple imputation using Fully Conditional Specification (FCS) implemented by the MICE algorithm as described in Van Buuren and Groothuis-Oudshoorn (2011).

Let’s re-run the simple linear regression model above, but this time let’s create 20 imputed datasets, run 20 regression models and then pool the results. See FIMD Book Section 1.4

Compare these regression results to the models above. Notice that the “std.error” for the regression coefficients are larger than they were for the kNN results and closer to fitting the model with the original data.

library(mice)
imp <- mice(x, seed = 1, m = 20, print = FALSE)
fit <- with(imp, lm(Sleep ~ Dream))
summary(pool(fit))
         term estimate std.error statistic       df      p.value
1 (Intercept) 5.904120 0.7560889  7.808764 48.78611 3.858037e-10
2       Dream 2.326442 0.3216144  7.233638 45.29561 4.431364e-09
Look at one of the regression models from the impute data

We can “peek under the hood” to look at one of the individual imputed datasets by running the following code. If you’d like to look at another model just change 1 to another number up to 20 (since there were 20 imputations performed).

# see simple output
fit[["analyses"]][[1]]

# get summary detailed output
summary(fit[["analyses"]][[1]])

Call:
lm(formula = Sleep ~ Dream)

Coefficients:
(Intercept)        Dream  
      6.090        2.216  

Call:
lm(formula = Sleep ~ Dream)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.4782 -2.0541  0.0424  2.2630  9.3787 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   6.0897     0.7318   8.322 1.39e-11 ***
Dream         2.2158     0.2953   7.504 3.45e-10 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.407 on 60 degrees of freedom
Multiple R-squared:  0.4841,    Adjusted R-squared:  0.4755 
F-statistic: 56.31 on 1 and 60 DF,  p-value: 3.449e-10

4. Impact of Sampling Weights for Survey Data (brief intro)

see Missing Data in PRAMS module.

R Code For This Module

References

R Core Team. 2025. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Other Helpful Resources

Missing Data Resources

and

Other Helpful Resources